등가속도 운동 공식
등가속도란 가속도가 일정하다는 것을 의미하며 등가속도 상태에서 운동하는 것을 등가속도 운동이라고 한다.

처음속도라는것은 (시간) t=0 일때 물체의 속도를 가리킨다. 물체에 따라 어느정도 속도가 있는것도 존재하므로 항상 정지상태부터 생각할 필요는 없다. 움직이는 상태부터 생각할수도 있으며 이때에 처음부터 움직인다=속도가 있다 라고 할 수 있기 때문에 처음 속도 라는 개념이 등장하며 정지 상태에서 시작할때에는 처음속도=0 이라고 생각할 수 있다.
1번 공식은 v0(시작속도) 과 a(가속도) 와 t(시간) 를 이용하여 해당 시간대의 속도를 계산하는 공식이다.
속도의 단위를 m/s 라고 가정하고 물체가 정지상태에서 (시작속도=0) 2m/s2 의 가속도로 2s 시간이 흐른 이후의 속도를 계산하여 보자.
v = v0 + at
= 0m/s + 2m/s^2 * 2s
= 4m/s
float velocity_from_initspeedAndacceleration(float v0,float a,
float t)
{
return v0+(a*t);
}
Error: 단위를 통일시켜야 함을 주의하자
2번 공식은 v0(시작속도) 과 a(가속도) 와 t(시간) 를 이용하여 해당 시간대의 위치를 계산하는 공식이다.
마찬가지로 속도의 단위를 m/s 라고 가정하고 물체가 정지상태에서 (시작속도=0) 2m/s2 의 가속도로 2s 시간 동안 움직인다고 가정하고 계산하여 보자.
x = v0t + 1/2 + at^2
= 0m/s * 2s + 1/2 * (2m/s^2 * 2s * 2s)
= 1/2 * (2m/s^2 * 2s * 2s)
= 4m
float location_from_velocity(float v0,float a,
float t)
{
return v0*t + 0.5f * (a * (t*t));
}
2차원과 3차원으로 확장시켜 속도와 위치를 벡터로 표현하면 아래 그림처럼 회전 같은 움직임도 표현이 가능하다.
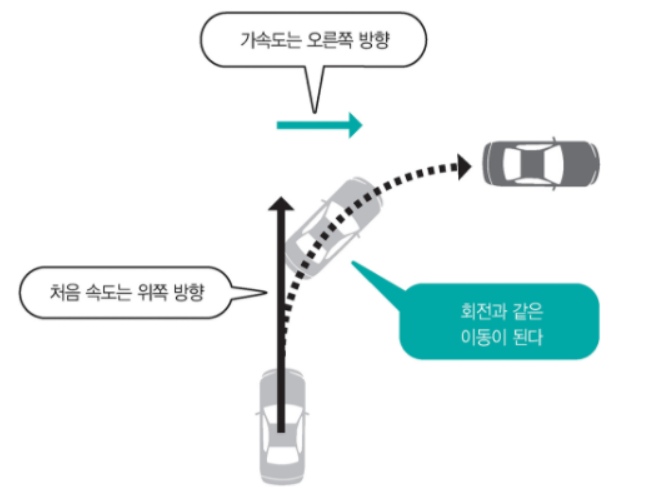
코드로 적용시키면 대충 요래 된다.
#include <iostream>
#include <type_traits>
inline namespace
{
template<typename T>
static constexpr T fps = T{ 60 };
template<typename T>
constexpr T dt = T{1} / fps<T>;
template<typename T>
void Move(T* pos, T* speed, T acceleration)
{
// 속도에 가속도를 누적한다.
*(speed) += acceleration;
// 좌표를 업데이트 한다.
*(pos) += *(speed);
}
template<typename T,auto Value>
constexpr T init_speed = T{ Value };
template<typename T>
constexpr T acc(const T value, uint32_t fps)
{
// 가속도 = m/s^2
return value / (fps * fps);
}
static void example()
{
using type = float;
//처음 속도 v0 = m/s = m * dt(1/fps);
type speed{ init_speed<type,20> *dt<type> };
type pos{ 0 };
// a = m/s^2
type acceleration = acc(type{ 2 }, fps<type>);
// 시뮬레이션
for (int i = 0; i < 100000; ++i)
{
Move(&pos, &speed, acceleration);
std::cout << " Position : " << pos << " Speed : " << speed<< std::endl;
}
}
}
int main()
{
example();
}