평면의 방정식

평면의 방정식

평면을 정의하기 위해서는 다음 조건중 하나만 만족하면 된다.

• 한 직선 위에 있지 않은 좌표가 3개 있다.
• 평면의 법선 벡터와 평면 위의 좌표가 하나 있다.

평면의 정의를 바탕으로 다음의 방정식을 사용한다.

a(x-x0) + b(y-y0) + c(z-z0) =0

여기서 (a,b,c) 는 평면의 법선벡터이며 (x0,y0,z0)는 평면 상의 한 점을 의미한다. (x,y,z)가 위 방정식을 만족하는 변수일때 (x,y,z) 는 평면 위의 좌표이다.

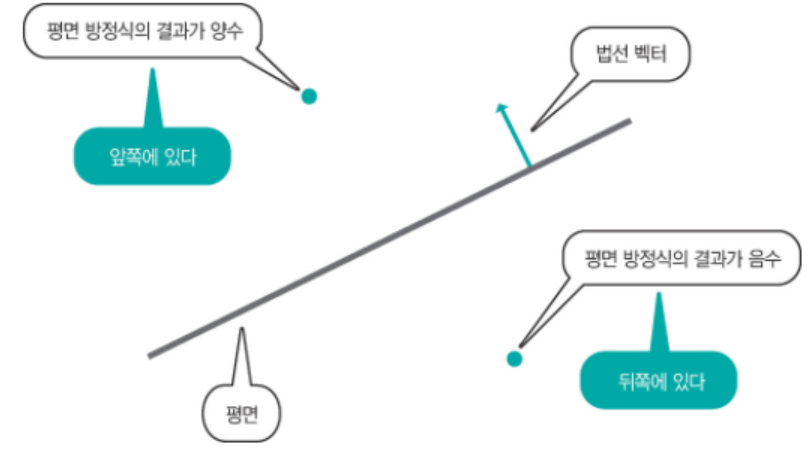
방정식의 값이 양수일때에는 평면의 법선벡터 좌표의 내적의 결과가 0 ~ π/2 사이라는 의미이다. 때문에 평면 안쪽에 존재한다고 해석하면 된다 (법선벡터가 가리키는 방향)

이 앞뒤 판단은 카메라 뷰 프러스텀을 평면으로 구성한 이후에 컬링할때에 자주 사용된다.

앞서 평면의 방정식을 언급하였는데 식을 전개하여서 간단히 만들어 보자.

• a(x-x0) + b(y-y0) + c(z-z0) = 0

• = ax + by + cz + -ax0 -by0 - cz0 =0

• = ax + by + cz + ( (-ax0) + (-by0) + (-cz0) ) =0

여기서 (ax0 + by0 + cz0) 는 평면의 법선과 평면상의 존재하는 임의의 한점의 좌표의 내적과 같으며 내적의 결과 값을 d 라고 하였을때 최종적으로 일반화한 식은 다음과 같다.

 = ax + by + cz + d =0

d는 평면상의 한 점 아무거나 대입해서 방정식을 세워서 전개하면 쉽게 구할수 있다. ax+by+cz = -d 여기서 x,y,z 는 평면상의 한 점이며 평면 법선의 정규화 여부에 따라 d 의 값이 달라지는 것에 신경쓰자

결과적으로 평면을 코드로 구현할때에는 다음과 같은식으로 구현한다.

1
2
3
4
5
6
7
8
9
10
11
12
13
struct plane  { float a,b,c,d; }
plane make_plane(vec3 n/*평면 법선*/,vec3 p,/*평면 임의의 점*/)
{
    // 평면의 법선을 정규화한다. 이러면 나중에 내적만으로 거리를 구할수 있어 편리하다.
    plane _plane;
    n = normalize(n);
    plane.a = n.x;
    plane.b = n.y;
    plane.c = n.z;
    plane.d = -dot(n,p);
     
    return plane;
}

프로그래밍적으로 구현할때에는 무한 평면을 의미하는 노멀벡터와 평면상의 한점의 내적의 음수값을 -d 로 사용하면 x,y,z 를 매개변수를 받아와서 손쉽게 평면기준 위치를 구할 수 있다

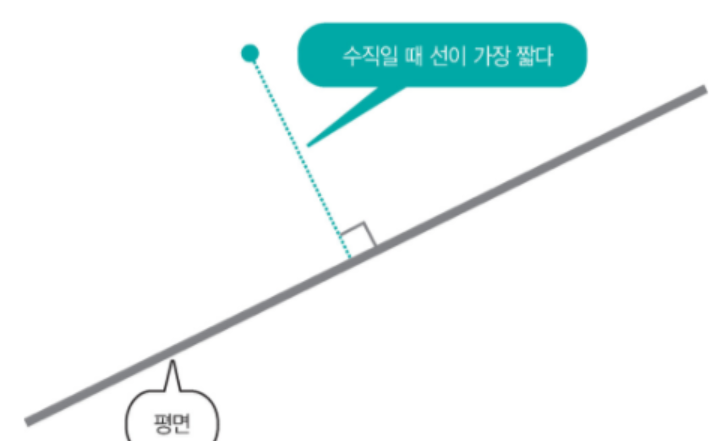
평면과 점의 최단거리는 평면의 법선벡터와 평면의 임의의 한점이 시점 구하고자 하는 점을 종점으로 하는 벡터를 만든 이후 두 벡터의 내적의 결과값을 평면의 법선벡터의 길이로 나누면 된다.

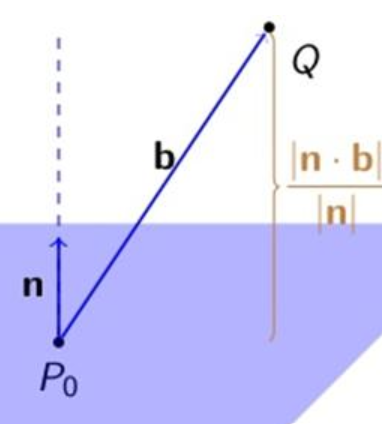
첨부한 그림에는 평면의 한점과 법선의 시점이 일치하지만 꼭 일치해야할 필요는 없다 (평면상의 한점이면 됨)

1
2
3
4
5
6
7
8
float Distance_PlaneToPoint(vec3 n /*평면 법선*/,vec3 p/*평면위의 점*/,
vec3 pos /*구하고자 하는 점*/)
{
	float d = 	-dot(n,p);
	//평면 법선이 정규화 되어있다면 반환값은 평면과 점의 최단거리를 의미한다.
	// 정규화 되어있지 않을수도 있으므로 길이로 나누어준다.
	return dot(n,pos) + d) / length(n);
};

귀찮아서 세 점은 언급 안했는데 세 점으로 벡터 두개 만들어서 외적(평면 법선)하면 끝남 여기서 세 점의 외적순서로 평면의 앞뒤가 결정된다. 여기서 조심해야 되는게 세 점이 한 직선 위에 있다면 (선형종속) (Rank 1 공간) 외적벡터가 영벡터가 튀어나오므로 평면을 정의할수 없음.

마지막으로 공식 정리

• 평면 방정식 ax + by + cz + d = 0 x,y,z 가 위 방정식을 만족할때 x,y,z 는 평면상의 한 점이다.
• 평면과 점의 거리 = (ax + by + cz + d)/sqrt( a^2 + b^2 + c^2 ) 이지만 평면의 법선벡터를 정규화 해준다면 = -(ax + by + cz + d) 으로도 식은 성립한다.