피타고라스의 정리를 증명 해보자.
증명하기 위해 밑변이 b 높이가 a 빗변이 c인 삼각형을 정의하고 해당 삼각형의 밑변과 높이의 합들로 이루어진 정사각형 안에 해당 삼각형의 빗변들로 이루어진 정사각형을 그려준다.
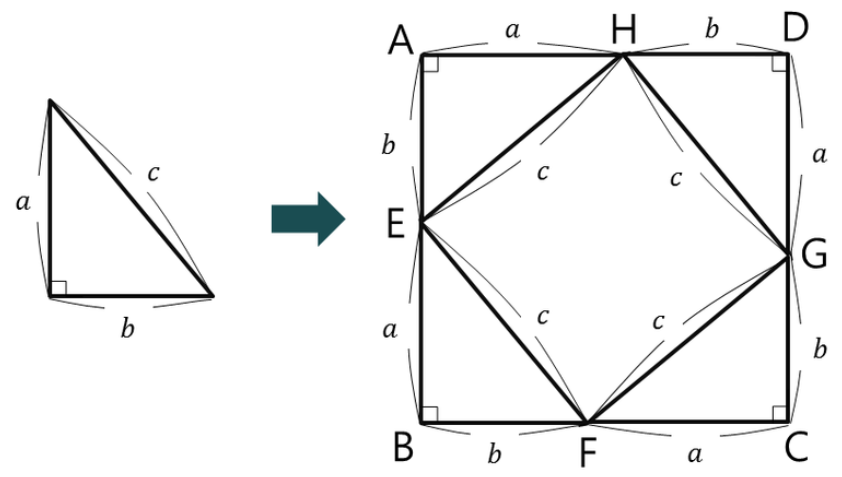
요렇게
이런 사각형이 있다고 치면 ABCD 꼭짓점으로 이루어진 사각형의 넓이는 모든 삼각형의 넓이의 합과 HGFE 사각형 넓이의 합과 같다고 볼 수 있다.
이것을 수식으로 표현하면 다음과 같다.
여기서 각 항을 곱셈공식으로 정리해주면 싱겁게 끝난다(…..)
- ABCD 사각형의 넓이 = 4개 직각삼각형 넓이 + 정사각형 HGFE 넓이
- (a + b)² + 4 ½ab + c²
- a² + 2ab + b² = 2ab + c² ! 여기서 공통된 2ab 를 없애주면 끝.
- a² + b² + c²