일반 삼각형에서의 사인과 코사인

일반 삼각형의 사인 법칙

일반 삼각형에서 각 변의 길이와 마주 보는 각의 크기에 대한 사인 값에 대하여 다음과 같은 관계가 성립한다.

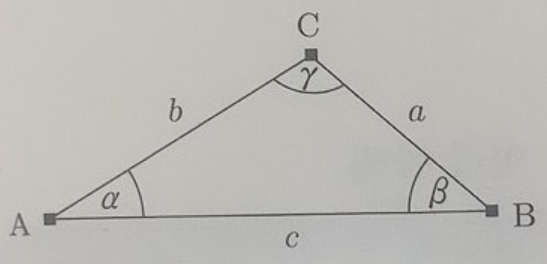
a/sin(α) = b/sin(β) = c/sin(γ) 

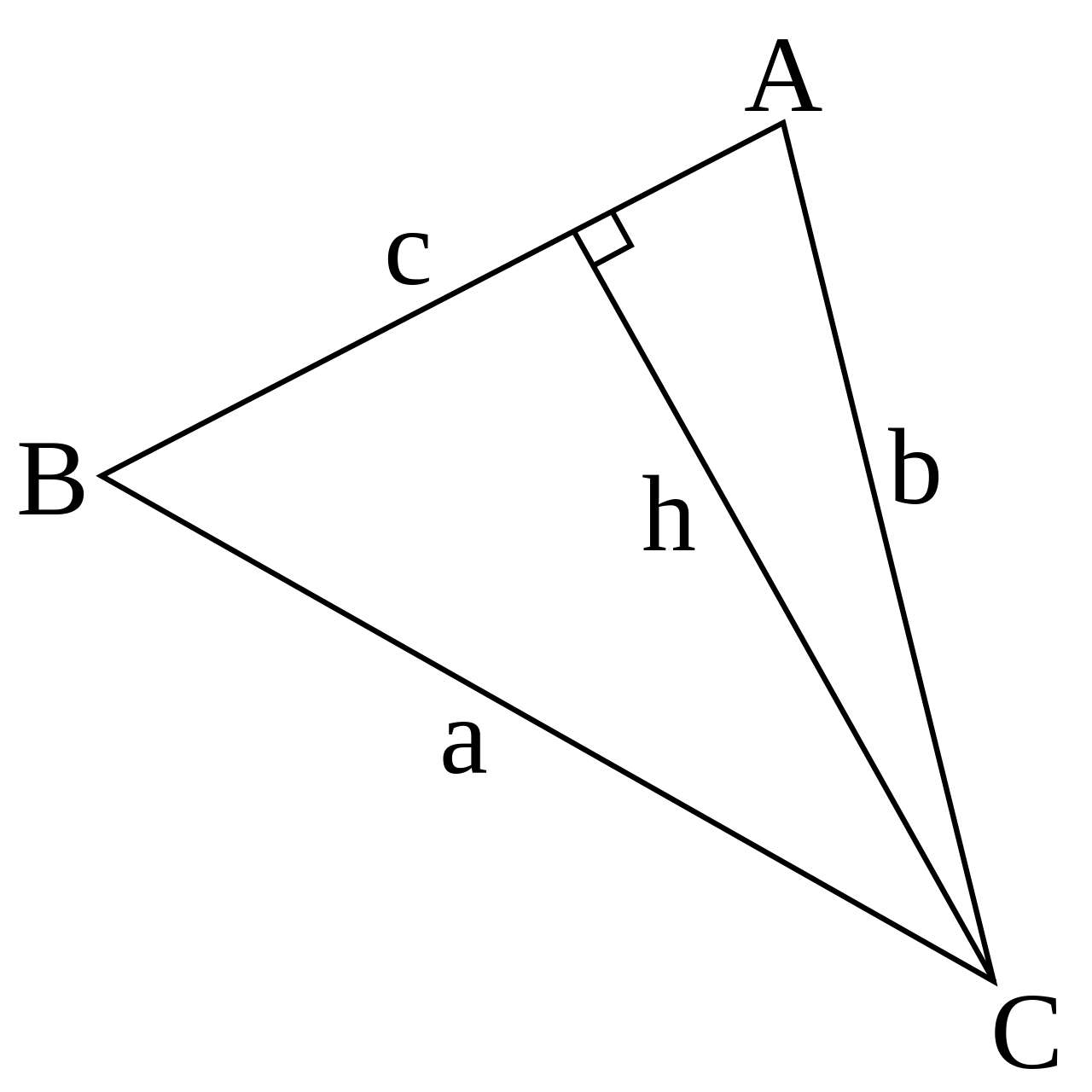
왜 이런 관계가 성립하는지는 삼각형의 넓이를 통한 증명을 통해 알 수 있다.

해당 삼각형의 넓이는 ½ch 이다. 삼각법에 따르면 h = b sin(A) 이며 삼각형 ABC 의 넓이 K는 다음과 같다.

K = 1/2ch = 1/2bc sin(A)
2K = bc sin (A) = ac sin (B) = ab sin(C)
여기서 abc 로 각 항을 나눠주자.
bc sin (A) / abc = ac sin(B) / abc  = ab sin(C) / abc
= sin(A) / a = sin(B) / b  = sin(C) / c 

여기를 참고하면 증명에 대해 더 알 수 있다. 외적으로도 증명할 수 있다.

이 법칙은 다음과 같이 표현 할 수도 있다. 두 변의 길이의 비는 각 변과 마주 보는 각의 크기에 대한 사인값의 비와 같다.

그 이유는 곱셈법칙으로 쉽게 알 수 있다.

a/sin(α) = b/sin(β) <=> a = b sin(α) / sin(β)  <=> a/b = sin(α)/sin(β) 이를 다른 변의 길이와 마주 보는 각의 크기의 비에 적용하면 똑같은 결과를 얻는다.

a/b = sin(α)/sin(β)
b/c = sin(β)/sin(γ)
a/c = sin(α)/sin(γ)

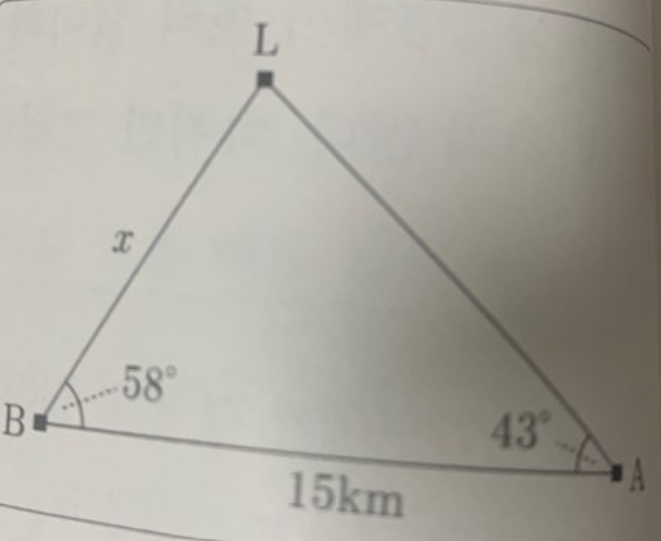
해당 삼각형에서 두 각과 두 각 사이의 선분의 길이를 알고있다. 여기서 x의 길이를 앞에서 배운 법칙을 사용해 구해보자.

먼저 삼각형의 두 각을 알고 있으니 나머지 한 각은 손쉽게 구해진다.

γ = 180 - 43 - 58 = 79

이제 앞서 배운 법칙을 사용하자.

case a : x / 15 = sin(43) / sin(79)  <=>  x =  15 sin(43) / sin(79) = 10.42
case b : x / sin(43) = 15 / sin(79) <=> x = 15 sin(43) / sin(79) = 10.42

일반 삼각형의 코사인법칙

일반 삼각형의 코사인 법칙에서 중요한 것은 각 변의 길이 사이의 관계이다. 이때 적어도 한 개의 각의 크기는 알고 있어야 한다. 두 변의 길이와 그 사이의 끼인각의 크기를 알면 코사인 법칙을 항상 적용할 수 있다.

a² = b² + c² - 2bc cos(α)
b² = a² + c² - 2ac cos(β)
c² = a² + b² - 2ab cos(γ)

이번에는 벡터의 내적을 이용해서 증명 해보자.

증명을 하기에 앞서 잠깐 벡터의 내적에 대해 조금만 살펴보자.

A · B= |A| |B| cos (θ) 여기서 theta 는 두 벡터사이의 각이다.

동일한 벡터는 각이 0 라디안이고 cos(0) 의 값은 1이기 때문에 다음이 성립한다.

|A|²= A·A

이제 본격적으로 증명 해보자.

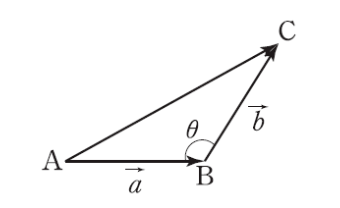
다음과 같은 삼각형이 있다. 여기서 꼭짓점 A가 시점 B가 종점인 벡터는 a B에서 C인 벡터는 b이다. 그럼 벡터 c는 다음과 같다.

c = a + b

|c|^2 = |a+b|^2
= |a|^2 + 2a ·b +|b|^2
= |a|^2 + 2|a||b|cos(180-θ) + |b|^2
 
 이때  cos(180 - θ)  = -cos θ 이므로

이므로 코사인 법칙이 성립함을 알 수 있다.