광선과 평면의 교차점

n은 평면의 노말, p1는 평면 상의 임의의 점 d는 음의 부호를 가진 원점에서 평면까지의 최단거리 p는 광선의 시작점 L은 광선의 방향 s는 광선이 평면과 만났을때의 교차점이라 하며 마지막으로 t는 ||s-p|| 라 한다.

평면의 정의 \(n\cdot p1+d=0\) \(d= -(n \cdot p1)\)

1. t가 p에서 s까지의 거리이니 s는 p+ tL 이다.
2. L과 p는 이미 정의한 값이므로 t만 구하면 s를 구할 수 있다.

결론부터 얘기하고 들어가자면 t는 \(\frac{-d -n \cdot p}{n \cdot L}\)이다.

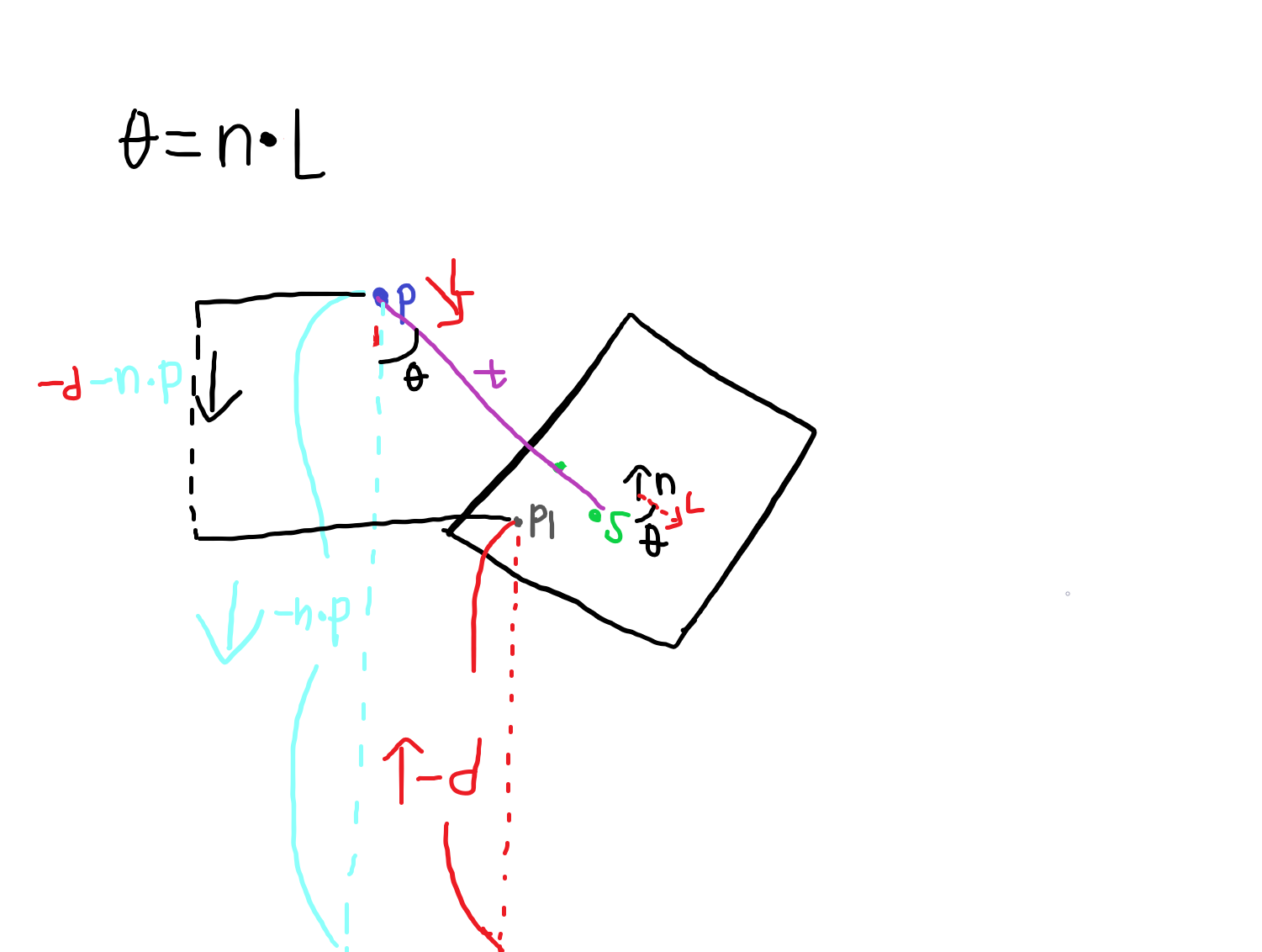
\(-d -n \cdot p\)

광선의 시작점과 평면사이의 최단거리 이다. 점을 평면에 투영한 거리 (음의부호) 와 원점에서 평면까지의 최단거리 (-d) 를 더해서 나오는 것.

\(n \cdot L\)

광선과 노말을 내적해 코사인을 구한다.

그림을 보면 t는 삼각형의 빗변에 해당한다. t를 구하기 위해 삼각형의 밑변을 구한 이후에 내적을 통해 구한 cos로 나눠줘서 빗변의 길이를 구하는 것. n과 L의 내적을 통해 나온 각과 \(-d -n \cdot p\)를 밑변으로 하고 t를 빗변으로 하는 삼각형의 각은 동일하기 때문에 가능하다.