원근 투영 행렬

아래의 행렬은 왼손 좌표계 기준 (행 기준 행렬)

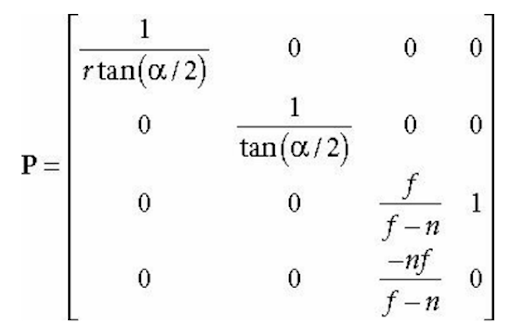
NDC = Normalize Device Coordinate (정규화된 장치 좌표)

x,y 는 -1 ~ 1 범위 좌표를 가지며 z는 0~1 범위 로 정규화된 좌표 시스템. 범위를 벗어난 좌표는 근평면과 먼평면 그리고 시야각으로 정의된 절두체에서 벗어난 좌표를 의미한다.

Far 는 카메라의 Z 축 기준 먼 평면 Near는 카메라의 Z축 기준 근 평면 Fov는 카메라의 시야각

\(r = Aspect = \frac{Width}{Height}\) \(f = Far\) \(n= Near\) \(\alpha = Fov = Field Of View\)

원근 투영 행렬로 변환된 위치 벡터는 이후에 4번째 원소 w로 x,y,z 를 나눠주는 작업을 거치며 해당 작업 이후에 화면상에 출력 되는 좌표는 NDC 좌표를 가져야 한다.

아래 식에서 v는 위치 벡터이므로 w는 1 \(v(x,y,z,w) ProjMatrix = v'(x',y',z',w')\) \(v.w = 1\)

### 3행 4열이 갖는 의미 왜 변환후 w’ 원소는 변환전 z와 값이 같은가

3차원 좌표를 2차원 좌표로 투영할때에 원근감을 표현 하기 위해서는 카메라를 기준으로 해서 멀리 떨어져 있는 물체는 보다 작게 그려야 한다.

물체가 점점 작게 축소됨과 동시에 소실점 (화면의 중앙)에 점점 가까워 진다.

이러한 소실점을 표현하기 위해서는 x,y 좌표를 z 로 나누어 주어야 하는데 z원소 또한 후에 깊이 버퍼에서 사용할때에 0~1로 정규화된 좌표로 사용해야 하므로 z’ 을 여기에 사용할수는 없다.

때문에 4번째 원소를 사용하는 것이다. 변환후에 4번째 원소인 w’ 를 z와 똑같은 값으로 변환함으로써 w’ 으로 x’ y’ z’ 를 나눌수 있고 변환 이후의 x’‘,y’‘,z’’ 는 NDC 좌표로 변환이 되었다고 볼 수 있다.

\(\frac{f}{f-n} z ,\frac{-nf}{f-n}w , w=1\)

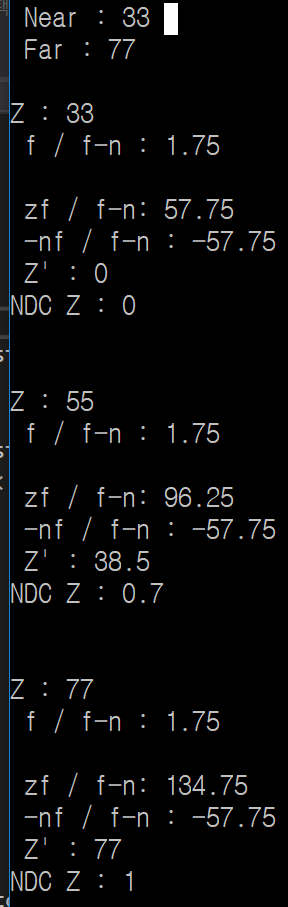
Z를 0~1로 정규화 하기위한 작업 w원소가 1이므로 z’ 은 zf / (f-n) + -nf / (f-n) 으로 결정 되는데 z가 근평면에 걸쳐있다면 후에 z나누기까지 변환 이후에 0이 나와야 하며 먼평면에 걸쳐있다면 1이 나와야 함.

근평면에 걸쳤을 때 , 먼평면에 걸쳤을 때 \(\frac{z'}{w'}=0 , \frac{z'}{w'}=1\)

근 평면에 위치해 있을시의 z는 near와 같으므로 \(\frac{zf}{f-n} + \frac{-nf}{f-n} = \frac{nf}{f-n} + \frac{-nf}{f-n} =0 = z' = \frac{z'}{w'}\) 근평면에 위치한 z 는 z’ 로 변환된 직후부터 (깊이 나누기 수행 전) 0 이므로 깊이 나누기 수행시에 w’ 이 무엇이든 간에 0이다. NDC 좌표로 변환이 잘 되는것을 볼 수 있다.

먼 평면에 위치해 있을시의 z는 far 와 같으므로 \(\frac{zf}{f-n} + \frac{-nf}{f-n} = \frac{f^2}{f-n} + \frac{-nf}{f-n} = \frac{f^2 -nf}{f-n} = \frac{f(f-n)}{f-n} = f = z = z' =w'\)

변환 이후의 좌표 z’는 far 와 같으며 far 는 z와 같으므로 z’ 도 z와 같고 w’ 는 z와 같으므로 \(f= z = z' =w'\) 때문에 이후에 깊이 나누기 수행시 (z’/w’) 1이 나오게 된다. 먼평면에 위치한 z가 NDC 좌표 1로 변환이 잘되는 것을 알 수 있다.

\(\frac{1}{tan(\alpha/2)}\)

종횡비를 의미하는 r 은 좀 있다가 살펴봄.

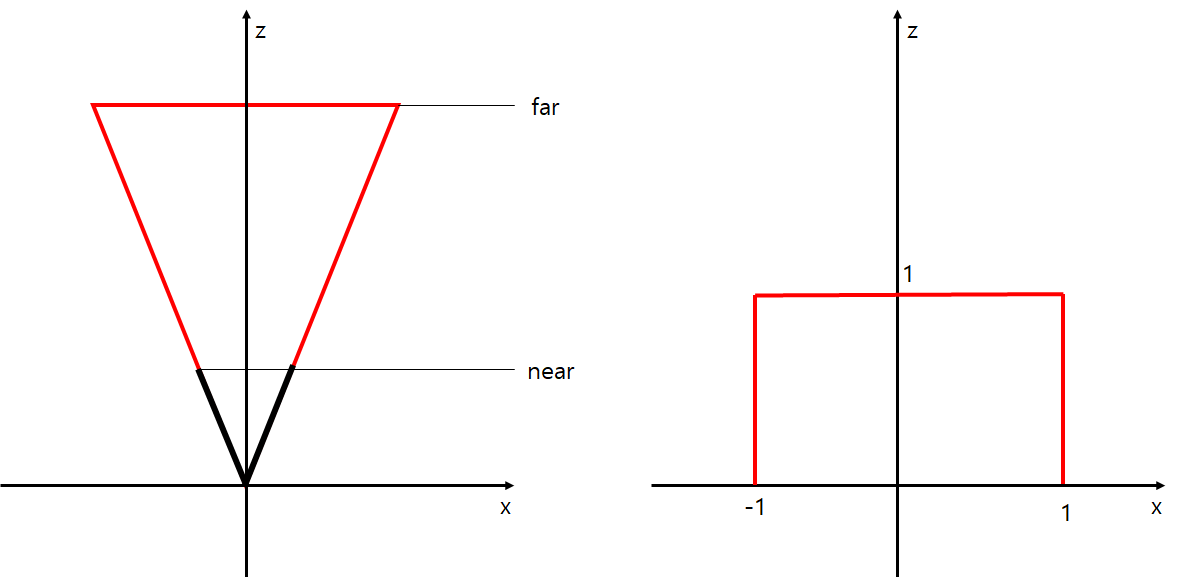
(알맞는 그림을 못찾겠음)

카메라의 원점에서 z축에 비스듬히 뻗어 나가는 대각 선분과 원점에서 z축 방향으로만 뻗어나간 선분으로 삼각형 두개를 만들 수 있으며 그리고 해당 삼각형은 같은 각을 공유하며 세타는 시야각의 절반인것도 알 수 있다. \(\theta = \alpha /2\)\(\tan(\pi/4) =1\)

변환이후의 x’ 은 변환전 x 를 tan 로 나눈다.

시야각이 커지면 절두체의 삼각형의 세타도 커지며 tan 함수의 값도 커진다.x를 tan로 나누므로 이것은 변환이후의 x’ 의 값이 시야각에 반비례 해서 커지거나 작아진다는 것을 의미한다.

x’ 을 w’ 로 나눴을때의 좌표가 NDC 좌표이므로 x’ 의 값이 커진다는 것은 -1~1 범위로 나타낼 수 있는 수들의 범위가 좁아진다는 것을 의미하며 x’ 의 값이 작아진다는 것은 그 반대이고 이것을 통해 시야각의 조절을 통한 화면으로 출력되는 범위를 조절 할 수 있다.

디그리 기준 Far 가 500 Near가 100 이라 가정하고 한번 해보자. 탄젠트가 45도 일때와 60도일때 30 도일때를 비교해보자

45도일때 \(\tan(45 degree) =1\)

Far 평면에 위치했을 때

밑변 높이 비율이 같다는 것이므로 해당 xy평면에 위치하는 물체들의 x,y 좌표가 먼 평면의 좌표보다 같거나 작아야지만 -1 ~ 1 로 변환됨. \(x=300,y=400 ,z=500\) \(x' = x / tan(45 degree) = x'/1 = x' =300\) \(y' = y / tan(45 degree) = y'/1= y' =400\) \(x'' = x'/w' = 300/500 = 0.6 , y'' = y'/w' = 400/500 = 0.8\)

Near 평면에 위치 했을 때

\(x=300,y=400 ,z=100\) \(x'' = x'/w' = 300/100= 3, y'' = y'/w' = 400/100 = 4\) 좌표가 NDC를 벗어나서 화면에 출력되지 않음

30도일때 \(\tan(30 degree) =0.57\)

Far 평면에 위치했을 때

높이가 밑변보다 큰 상황 xy평면에 위치하는 물체들의 x,y 좌표의 스케일이 탄젠트 비율에 반비례해 커진다. \(x=300,y=400 ,z=500\) \(x' = x / tan(30degree) = x'/0.57 = x' =519.61\) \(y' = y / tan(30 degree) = y'/0.57 = y' =701.75\) \(x'' = x'/w' = 519.61/500= 1.03 , y'' = y'/w' = 701.75 /500= 1.40\) 45도일때는 출력되는 좌표였지만 XY 좌표가 커져서 깊이 나누기 수행 이후 NDC를 벗어나서 화면에 출력되지 않음

Near 평면에 위치 했을 때

\(x=300,y=400 ,z=100\) \(x'' = x'/w' = 519.61/100= 5.19 , y'' = y'/w' = 701.75 /100= 7.01\)

60도일때 \(\tan(60 degree) =1.73\)

Far 평면에 위치했을 때

밑변이 높이보다 큰 상황 xy평면에 위치하는 물체들의 x,y 좌표의 스케일이 탄젠트 비율에 반비례해 작아진다. \(x=300,y=400 ,z=500\) \(x' = x / tan(60 degree) = x'/1.73 = x' =173.41\) \(y' = y / tan(60 degree) = y'/1.73 = y' =231.21\) \(x'' = x'/w' = 173.41/500= 0.34 , y'' = y'/w' = 231.21/500= 0.46\) 화각이 커져서 물체가 45 도 일때보다 원점으로 더욱 소실되고 작아짐

Near 평면에 위치 했을 때

\(x=300,y=400 ,z=100\) \(x'' = x'/w' = 173.41/100= 1.73 , y'' = y'/w' = 231.21/100= 2.31\) 출력 X

## 종횡비 \(\frac{1}{r tan(\alpha/2)}\) x 에서 x’ 으로 변환될 때 종횡비로 나누어 주는데 화면에 출력되는 가로 축을 조절하기 위함.

종횡비가 1:1 즉 모니터의 가로세로 비율이 똑같다면 종횡비를 고려할 필요는 없지만 대부분의 모니터는 4:3 16:9 16:10 등 다양한 종횡비를 가지고 있고 대부분 가로 축이 길다. 때문에 Width/Height 으로 비율을 구한 이후 그 값으로 x을 나누어주면 x’ 범위가 종횡비에 반비례해 좁아지거나 커짐.

당연히 NDC 공간의 들어갈 수 있는 범위도 종횡비에 비례해서 확장되거나 축소됨.

가로가 세로에 비해 넓다면 비례가 1보다 크므로 범위가 확장되고 세로가 크다면 비례가 1보다 작으므로 축소되는 효과를 가져옴.